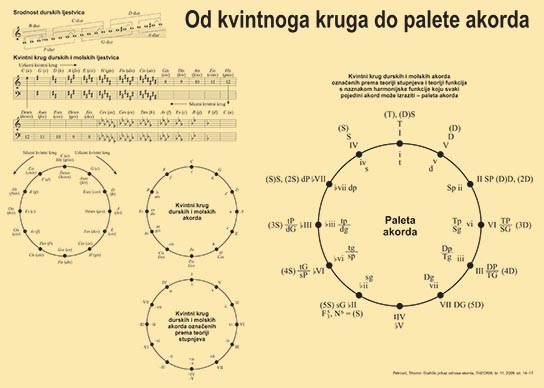
Paleta akorda
Paleta akorda grafički je prikaz odnosa akorda, koji uključuje njihove nazive i harmonijsku funkciju koju mogu izraziti u tonalitetu. Paleta akorda nastaje na temelju kvintnoga kruga, kako je prikazano na slici, lijevo gore. Srodnost se između C-durske i G-durske ljestvice može protegnuti i na C-durski i G-durski akord i tome slično. Uz durske se akorde mogu na iste točke kvintoga kruga smjestiti i drugi akordi s istim osnovnim tonom. Tako će se, primjerice, C-durski i c-molski akord u prikazu naći na istome mjestu, a njihove se oznake – veliko slovo abecede za durski i malo slovo za molski akord – mogu napisati uz istu točku kvintnoga kruga (v. sl. u kojoj piše: Kvintni krug durskih i molskih akorda!). Iz slike se lako razumije da su akordi čiji su osnovni tonovi udaljeni za kvintu uzlazno ili silazno međusobno najsrodniji, jer su i na crtežu ti akordi najbliži jedan drugomu.
Ako C-durski akord na vrhu slike uzmemo za prvi stupanj C-durskoga tonaliteta, tada ga možemo označiti kako je uvriježeno, rimskim brojem (I). Pritom se može rabiti moderni način označavanja akorda prema teoriji stupnjeva, iz kojega se prema pisanju velikih ili malih slova prepoznaje vrsta akorda na isti način kao što je to i pri pisanju slovnih naziva akorda. Durski se akordi označavaju velikim slovima u ulozi rimskih brojeva (u C-duru C = I), a molski malim slovima (u c-molu Cm = c = i). U odnosu na akord I. stupnja svi ostali akordi, povezani u kvintni krug, mogu biti označeni kao stupnjevi unutar istoga tonaliteta, pa dalje, u C-duru, ispada ovako: F = IV, G = V, Fm = f = iv, Gm = g, Dm = d = ii, Am = a = vi itd. Alteracija se pritom može označiti na uobičajen način, znakovima + i – (v. Krug u kojemu piše: Kvintni krug durskih i molskih akorda označenih prema teoriji stupnjeva!) ili povisilicom i snizilicom (v. desnu stranu sl.!).
Na slici sasvim desno je kvintni krug durskih i molskih akorda označenih prema teoriji stupnjeva i teoriji funkcija s naznakom harmonijske funkcije koju svaki pojedini akord može izraziti ili tzv. Paleta akorda. Uz prethodno opisane brojevne oznake akorda prema teoriji stupnjeva (I / i = durski / molski kvintakord prvoga stupnja itd.) na toj su slici i slovne oznake, koje je u praksu uveo Hugo Riemann. Velikim su slovima označeni durski glavni kvintakordi tonaliteta, a malima molski: T = durski tonički kvintakord, t = molski tonički kvintakord, S = durski subdominantni kvintakord, s = molski subdominantni kvintakord, D = durski dominantni kvintakord, d = molski dominantni kvintakord.
Povezanost glavnih i sporednih kvintakorda raspoznaje se prema drugomu slovu u oznaci. Primjerice, Tp = molski akord paralelan durskom toničkom akordu ili tonička molska paralela, Tg = molski protuakord durskom toničkom akordu ili tonički molski protuakord itd. Tako je na mjestu a-molskoga akorda napisan broj vi (malim slovima, jer je molski akord) te oznaka Tp (jer je taj molski akord paralelan toničkome akordu, koji je po vrsti durski). Isti se akord može označiti i kao Sg (jer je taj molski akord istodobno i protuakord subdominantomu akordu, koji je po vrsti durski).
Svaki je glavni kvintakord nositelj jedne od triju harmonijskih funkcija, koje se označavaju velikim slovom u zagradi: (T) = tonička funkcija, (S) = subdominantna funkcija, (D) = dominantna funkcija.
Na slici su označeni i pojedini alterirani oblici akorda te njihova moguća harmonijska funkcija, koju opisujemo kao sekundarnu dominantnost ili sekundarnu subdominantnost.
Primjerice, (D)D ili 2D označava durski akord II. stupnja (SP), koji može izraziti dominantnu harmonijsku funkciju prema akordu V. stupnja, on dakle može biti dominanta od dominantnoga akorda ili tzv. dvostruka dominanta, i tome slično.
Akord sniženoga sedmog stupnja nosi uznaku 2S ili (S)S jer može izraziti subdominantnost u odnosu na subdominantni akord, tj. može biti subdominanta subdominante ili dvostruka subdominanta, i tome slično.